UNIDAD 4: POLÍGONOS

En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se cortan se llaman vértices. El interior del polígono es llamado área.

ELEMENTOS DE UN POLÍGONO

En un polígono se pueden distinguir los siguientes elementos geométricos:

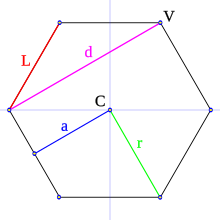
• Lado (L): es cada uno de los segmentos que conforman el polígono.
• Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
• Diagonal (d): es el segmento que une dos vértices no consecutivos.
• Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
• Semiperímetro (SP): es la mitad del perímetro.
• Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
• Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.

En un polígono regular se puede distinguir, además:

• Centro (C): es el punto equidistante de todos los vértices y lados.
• Ángulo central (AC): es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
• Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.

CLASIFICACIÓN de los polígonos según

1.- dirección de sus lados:

• Convexo, si todo segmento que une dos puntos cualesquiera del contorno del polígono yace en el interior de este. Todo polígono simple y con todos sus ángulos internos menores que 180º es convexo.
• No convexo, si existe un segmento entre dos puntos de la frontera del polígono que sale al exterior del mismo. O si existe una recta capaz de cortar el polígono en más de dos puntos.
• Cóncavo, si es un polígono simple y no convexo.
• Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.

2.- la magnitud de sus lados y sus ángulos:

• Equilátero, si tiene todos sus lados de la misma longitud.
• Equiángulo, si tiene todos sus ángulos interiores iguales.
• Regular, si es equilátero y equiángulo a la vez.
• Irregular, si no es regular. Es decir, si no es equilátero o equiángulo.

3.- la circunferencia:

Cíclico, si existe una circunferencia que pasa por todos los vértices del polígono. Todos los polígonos regulares son cíclicos: 

• Inscriptibles, cuando es interior a una circunferencia que pasa por sus vértices.
• Circunscriptibles, si tiene una circunferencia interior tangente a sus lados