Hoy he visto el vídeo que ha hecho Pedro Moraelche de Ladis, profesor y compañero del instituto. Cuando le conocí, me llamo la atención su cercanía, su capacidad de ponerse en el lugar del otro. Yo también quiero recordarle y por esto quiero compartir este vídeo.
Donde estés... un abrazo.
Ladis from Mairit21 on Vimeo.
martes, 20 de enero de 2015
sábado, 17 de enero de 2015
LAS FORMAS EN LA NATURALEZA
Os dejo un material que ha elaborado su autor a partir de la exposición que hubo hace unos años en Caixa Forum sobre las formas en la naturaleza. Creo que la reflexión que se hizo sobre nuestro entorno es muy interesante.
Seguro que os gusta.
UNIDAD 4: POLÍGONOS REGULARES CONVEXOS Y ESTRELLADOS
Un polígono convexo es una figura en la que todos los ángulos interiores miden menos de 180 grados y todas sus diagonales son interiores.
Cualquier recta que pase por un lado de un polígono convexo deja a todo el polígono completamente en uno de los semiplanos definidos por la recta. Un polígono es convexo solo si cualquier segmento entre dos puntos que estén dentro del mismo está dentro, es decir el segmento no corta los lados. En un polígono convexo, todos los vértices "apuntan" hacia el exterior del polígono.
Cualquier recta que pase por un lado de un polígono convexo deja a todo el polígono completamente en uno de los semiplanos definidos por la recta. Un polígono es convexo solo si cualquier segmento entre dos puntos que estén dentro del mismo está dentro, es decir el segmento no corta los lados. En un polígono convexo, todos los vértices "apuntan" hacia el exterior del polígono.
Como se ha indicado un polígono es regular si tiene sus lados iguales y sus ángulos iguales.
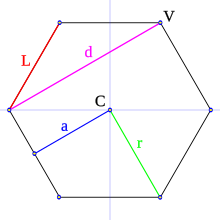
 | En la figura se muestran los elementos más importantes de un polígono regular. Radio (r): segmento que une el centro con un vértice. Es el radio de la circunferencia circunscrita. Apotema (a): Segmento que une el centro con el punto medio de un lado. En un polígono regular de n lados: Angulo central =360/n Angulo interior = 180 - 360/n Área = Perímetro x Apotema /2; A = n· L · a /2 , ya que es el área de n triángulos de base L y altura a (L/2)2 + a2 = r2 por ser triangulo rectángulo L/2, r y a |
Un caso de estos polígonos regulares son los polígonos estrellados. Estos, se obtienen a partir del regular convexo, uniendo vértices no consecutivos y recorriendo todos los vértices de forma continua.
Vuelvo a dejaros el material de Juan Díaz Almagro.
UNIDAD 4: CUADRILÁTEROS
Siguiendo el material elaborado por Juan Díaz Almagro, os presento el bloque correspondiente a los Cuadriláteros.
UNIDAD 4: TRIÁNGULOS
Os dejo un material interesante del profesor Juan Díaz Almagro donde podéis estudiar las características de los triángulos y donde encontraréis un número importante de construcciones.
UNIDAD 4: POLÍGONOS
En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se cortan se llaman vértices. El interior del polígono es llamado área.
ELEMENTOS DE UN POLÍGONO
En un polígono se pueden distinguir los siguientes elementos geométricos:
En un polígono regular se puede distinguir, además:
CLASIFICACIÓN de los polígonos según
2.- la magnitud de sus lados y sus ángulos:
ELEMENTOS DE UN POLÍGONO
- Lado (L): es cada uno de los segmentos que conforman el polígono.
- Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
- Diagonal (d): es el segmento que une dos vértices no consecutivos.
- Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
- Semiperímetro (SP): es la mitad del perímetro.
- Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
- Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.
- Centro (C): es el punto equidistante de todos los vértices y lados.
- Ángulo central (AC): es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
- Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
CLASIFICACIÓN de los polígonos según
1.- dirección de sus lados:
- Convexo, si todo segmento que une dos puntos cualesquiera del contorno del polígono yace en el interior de este. Todo polígono simple y con todos sus ángulos internos menores que 180º es convexo.
- No convexo, si existe un segmento entre dos puntos de la frontera del polígono que sale al exterior del mismo. O si existe una recta capaz de cortar el polígono en más de dos puntos.
- Cóncavo, si es un polígono simple y no convexo.
- Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.
- Equilátero, si tiene todos sus lados de la misma longitud.
- Equiángulo, si tiene todos sus ángulos interiores iguales.
- Regular, si es equilátero y equiángulo a la vez.
- Irregular, si no es regular. Es decir, si no es equilátero o equiángulo.
Cíclico, si existe una circunferencia que pasa por todos los vértices del polígono. Todos los polígonos regulares son cíclicos:
- Inscriptibles, cuando es interior a una circunferencia que pasa por sus vértices.
- Circunscriptibles, si tiene una circunferencia interior tangente a sus lados
Suscribirse a:
Entradas (Atom)