8 escalas1 from Fesquiro
miércoles, 19 de noviembre de 2014
TRIÁNGULO DE ESCALAS
Partiendo de un triángulo podemos crear cualquier tipo de escala gráfica, tanto de reducción como de ampliación. Podemos hacerlo de dos formas distintas: mediante el trazado de un triángulo equilátero de, por ejemplo 10 centímetros de lado, o dibujando uno isósceles cuyos catetos midan, igualmente, 10 centímetros.
ESCALAS TRANSVERSALES
Para obtener una mayor exactitud en la aplicación de una escala, puede construirse la escala transversal o de décimas, en la cual se pueden apreciar perfectamente las décimas de la unidad adoptada.
ESCALAS
La representación de objetos a su tamaño natural no es posible cuando éstos son muy grandes o cuando son muy pequeños. En el primer caso, porque requerirían formatos de dimensiones poco manejables y en el segundo, porque faltaría claridad en la definición de los mismos.
Esta problemática la resuelve la ESCALA, aplicando la ampliación o reducción necesarias en cada caso para que los objetos queden claramente representados en el plano del dibujo.
Se define la ESCALA como la relación entre la dimensión dibujada respecto de su dimensión real, esto es:
E = dibujo / realidad
Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será de reducción en caso contrario. La escala 1:1 corresponde a un objeto dibujado a su tamaño real (escala natural).
Esta problemática la resuelve la ESCALA, aplicando la ampliación o reducción necesarias en cada caso para que los objetos queden claramente representados en el plano del dibujo.
Se define la ESCALA como la relación entre la dimensión dibujada respecto de su dimensión real, esto es:
E = dibujo / realidad
Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será de reducción en caso contrario. La escala 1:1 corresponde a un objeto dibujado a su tamaño real (escala natural).
ESCALAS GRÁFICAS
Basado en el Teorema de Thales se utiliza un sencillo método gráfico para aplicar una escala.
Véase, por ejemplo, el caso para E 3:5
1º) Con origen en un punto O arbitrario se trazan dos rectas r y s formando un ángulo cualquiera.
2º) Sobre la recta r se sitúa el denominador de la escala (5 en este caso) y sobre la recta s el numerador (3 en este caso). Los extremos de dichos segmentos son A y B.
3º) Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.

Véase, por ejemplo, el caso para E 3:5
1º) Con origen en un punto O arbitrario se trazan dos rectas r y s formando un ángulo cualquiera.
2º) Sobre la recta r se sitúa el denominador de la escala (5 en este caso) y sobre la recta s el numerador (3 en este caso). Los extremos de dichos segmentos son A y B.
3º) Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.
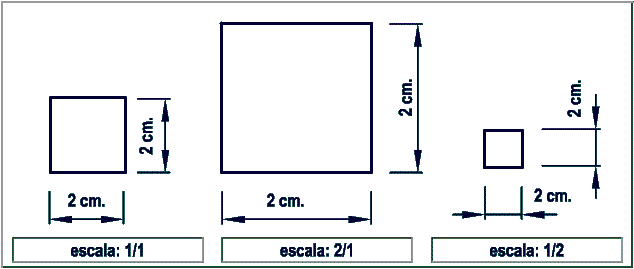
Cuadrado dibujado a 3 escalas diferentes

martes, 11 de noviembre de 2014
martes, 4 de noviembre de 2014
LA GEOMETRÍA SE HACE ARTE
En la historia de las matemáticas los árabes ocupan un papel nada despreciable. A ellos les debemos algo tan fundamental en nuestra cultura como los símbolos de los números tal como los utilizamos en la actualidad, con la aportación del "cero" que llegó directamente desde India hasta Europa.En este capítulo veremos cómo la Alhambra de Granada es una de las manifestaciones más importantes del arte geométrico.
Material didáctico de: http://www.rtve.es/television/la-aventura-del-saber/documentales/mas-por-menos/
UNIDAD 3: TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO
Transformación geométrica es una aplicación en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo plano.
A continuación se presenta el material elaborado por epvmanatiales sobre 4 transformaciones geométricas en el plano: Traslación, giro, simetría y homotecia.
LUGARES GEOMÉTRICOS: Conceptos
Estos ejercicios recogen los conceptos básicos que hemos trabajado en el examen parcial.
Suscribirse a:
Comentarios (Atom)

